本文简要先容代数学的早期发展，包括“代数”一词的由来、《九章算术》中的代数学内容，9世纪阿拉伯数学家花拉子密其东说念主过甚《代数学》的主要内容和影响。通过丰富的历史良友，咱们能对代数学的早期历史有更全面的意志。

撰文 | 郭园园（中国科学院天然科学史有计划所）

代数学是数学中最伏击的基础分支之一，代数学按照发展的先后轨则可分为初等代数学和综合代数学。初等代数学是指19世纪上半叶以前的方程表面，主要有计划某一方程（组）是否可解，如何求出方程整个的根（包括近似根）以及方程的根所具有的各式性质。19世纪末，代数学从方程表面转向代数运算的有计划，揭开了综合代数的序幕。

代数是如何发源的呢？代数之前已有算术。代数与算术主要区别在于代数要引入未知数，根据问题的条目列方程，然后解方程求未知数值。尽管古埃及、巴比伦、古希腊和古代中国等早期好意思丽中齐不错找到一些零星的代数学内容，但代数与算术在很长一段技术内是伴生在整个的。代数学发展成为一门落寞的数学分支应归功于中叶纪的阿拉伯东说念主。最早的代数学文章是9世纪初阿拉伯数学家花拉子密（Muhammad ibn Mūsā al-Khowārizmī，约780－约850）的《复原与抵消之书》（简称《代数学》，约820），它标志着初等代数学的诞生。

01

“代数”一词的由来

事实上，今天汉语中的“代数”一词并非源自中国古典数学，而是源自花拉子密《复原与抵消之书》（kitāb al-jabr wa-al-muqābala）的书名，其中的 “al-jabr”为“复原”。花拉子密将其界说为这么一种运算——将方程一侧的一个减去的量调养到方程的另一侧变为加上的量，举例5x+1=2-3x，变为8x+1=2，这便是一个“复原”历程。书名中“al-muqābala”的真谛是将方程两侧的同类正项消去，举例8x+1=2化为8x=1，这便是一个“抵消”历程。后世的阿拉伯数学家缓缓用“复原”一词来代替“复原与抵消”，粗略演化为今天方程化简中的移项与合并同类项。其后阿拉伯代数学传入欧洲，“复原（al-jabr）”一词演变为英文中“代数（algebra）”一词。

16世纪末，欧洲耶稣会布道士来华，揭开了明末清初西学东渐的序幕。清康熙五十一年（1712）前后，耶稣会士傅圣泽（Jean-Françoise Foucquet，1665-1741）初次将标志代数传入中国，为康熙天子撰写了《阿尔热巴拉新法》，其中“阿尔热巴拉”便是algebra（代数）的音译。此外，该词还有“阿尔朱巴尔”“阿尔热巴达”“阿尔热巴喇”等译法。对于上述汉文译名，晚清《中西闻见录》记录：

亚喇伯国算学书，有名曰阿喇热巴尔爱阿喇莫加巴喇者，考其扬名之意，即补足法，亦相消法，[阿喇者，其也，热巴尔能也，分数变为整数之算法也，莫加巴喇相对也，比拟也，极度也，即相互调换意也。]积年既多，取其补足相消意，仅呼为阿尔热巴喇。

康熙之后，阿尔热巴拉被歪曲为“东来法”，广为流传，为“西学东源”说张本。与此同期，康熙秉承泰州进士陈厚耀（1648-1722）“请定步算诸书以惠世界”的提议，于康熙五十一年（1712）下诏开蒙养斋（蒙养斋被西方称为中国皇家科学院），并赐梅文鼎（1633-1721）之孙梅瑴成（1681-1763）举东说念主头衔，充蒙养斋汇编官，会同允祉、允禄等开动编撰《数理精蕴》，至康熙六十一年（1722）奏凯。该书收集了明末传入中国的西方数学常识，并摄取了其时中算家们的一些有计划后果。《数理精蕴》下编卷31-36有“借根方比例”，先容多项式的加减乘除律例，引入加号、减号、等号、移项等见地，以用代数设施求高次方程的解。其卷31云，“借根方者，假借根数、方数以务实数之法也”。“根数”便是未知数，“方数”便是根数的正指数幂。梅瑴成合计“借根方”的西名“阿尔热巴达”为“东来法”，它是宋元时间的“立天元一”法传播到西域之后又再次传回的居品，这么明清之际传入的西方代数学“借根方”刺激了乾嘉学者对宋元数学文籍的发掘，进而为伟烈亚力（Alexander Wylie，1815-1887年）等西方学者对中西数学文化作比较、疏导和互鉴提供了可能。

自18世纪20年代起，布道士被不容在内地布道，直至烟土干戈后被动开埠之时，西方数学的传入基本中断，并一直不息到1850年前后。1847年，英国东说念主伟烈亚力来到上海学习汉文，1853年他用汉文编写了《数学发蒙》先容西方数学。伟烈亚力在《数学发蒙》序中说：“有代数、微分诸书在……”，这是第一次使用汉文“代数”一词当作数学分支的称呼。1859年，李善兰（1811-1882）与伟烈亚力衔尾翻译的《代微积拾级》和《代数学》发行。其中《代微积拾级》的原来为好意思国数学家罗密士（E .Loomis，1881-1889）1851年所著的《融会几何与微积分》。《代数学》的原来为英国东说念主棣么甘（Augustus De Mogan，1806-1871；该译名取自古籍，现一般译为德摩根）1835年所著的“Elements of Algebra”，译为汉文时定名为《代数学》，这是我国第一册以“代数学”定名的书。书中指出“代数”二字取意“以字代数”，即以甲乙丙丁诸元代已知数，以寰宇东说念主物诸元代未知数。译本中的代数术语源于中国的传统代数学天元术，然而否定“借根方”是“东来法”。《代数学》发行后的十几年，标志代数在中国的传播并不堪利。直到1872年，华蘅芳（1833-1902）与傅兰雅（John Fryer，1839-1928）衔尾翻译的《代数术》发行，西方标志代数才流行和传播开来。

02

花拉子密之前的代数学

与数字之间的算术运算比拟，初等代数学的精妙之处在于处理含有未知数问题的历程通常是机械化的：最初将所求未知数设为“某物”或“某量”（今天一般设为x），并设立方程；随后在将方程化简为圭臬时势的历程中，这个“某物”或“某量”不错像已知数一样参与运算，举例“移项”“合并”或“抵消”等，它不错取代东说念主脑原本需要进行的复杂条目分析历程。这就好像是用算盘进行算术运算，东说念主们专揽算盘的形制、口诀和机械的拨珠不错替代多数的脑力服务，从而不错长技术准确地计较。

有的读者一又友可能会感到有趣，早在2300年前，古希腊数学家欧几里得（Euclid，约公元前330-前275）就能在其所著的《几何原本》中惩办复杂的图形问题并奠定了今天几何学的基础，为什么上述看似“通俗”的代数想想却只可追思到公元9世纪初呢？事实上，更早的古希腊、古印度和古代中国的数学好意思丽中或多或少也齐不错找到上述初等代数的内容，底下以中国古典数学中《九章算术》方程章为例。

汉代成书的《九章算术》第八章所给方程术极端于现今的线性方程组解法，是《九章算术》最了得的数学建树之一。该章第一问提倡方程术，是全章的纲，本章18说念问题齐要用方程术惩办。第二问提倡损益术，是列方程的设施。第三问提倡正负术，是惩办消元历程中或方程自身出现负数时的处理设施，是方程术的必要补充。

若以x, y, z隔离示意《九章算术》第一问中上、中、下禾各一束的实的斗数，得到线性方程组：

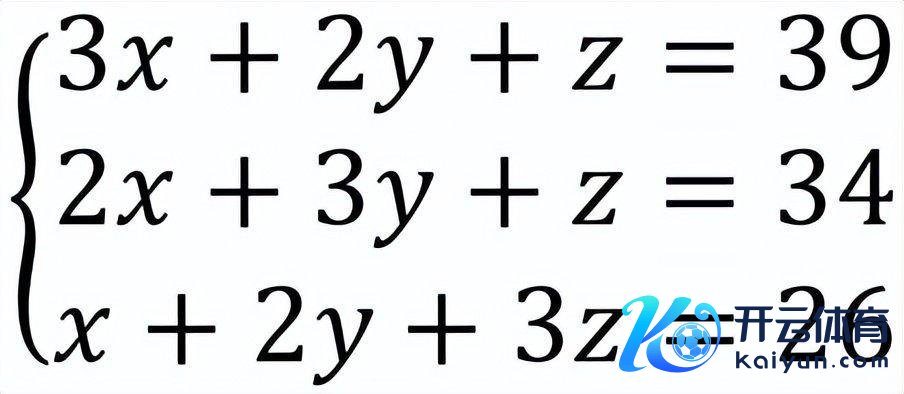
随后用直除法消元求解。所谓直除法便是整行与整行对减。此处方程的设立及消元变换领受位值制，每个数字不消标出它是什么物品的所有这个词，而是用所在的位置示意，与当代数学等分离所有这个词法一致。《九章算术》方程的示意，极端于列出其增广矩阵，消元历程极端于矩阵变换。举例第1问中的消元求解历程极端至今增广矩阵变换：

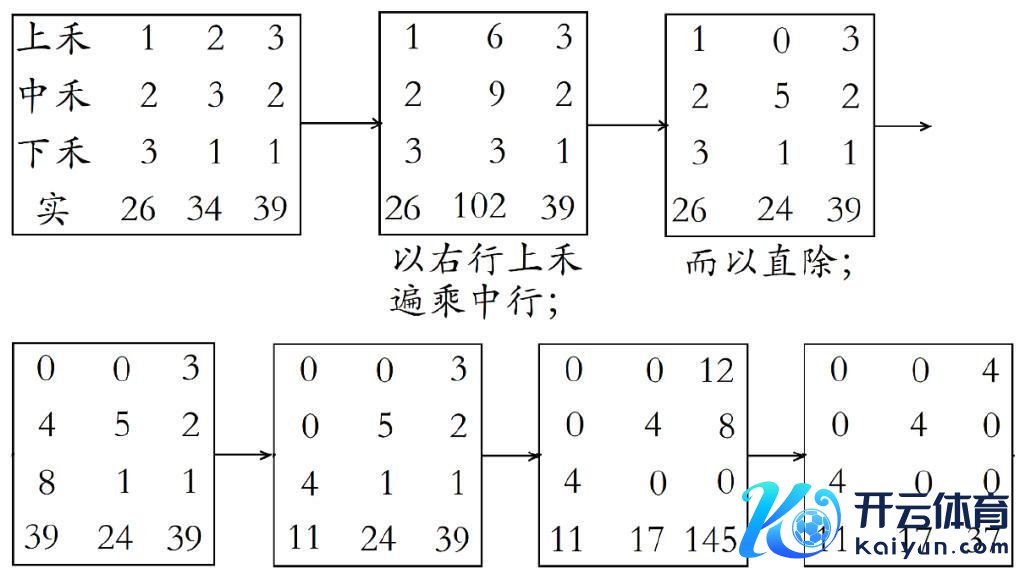
损益术是《九章算术》设立方程时要用到的伏击设施，方程章第二问提倡：损之曰益，益之曰损。“损之曰益”是说关系式一端损某量，极端于另一端益团结量；相通，“益之曰损”是说关系式一端益某量，极端于另一端损团结量。损益术极端于现今方程某项从等号一端向另一端移项，移项后窜改标志。举例第二问原题有：今有上禾七秉，损实一斗，益之下禾二秉，而实十一斗。若设上、下禾一秉之实隔离为x, y，极端于给出关系：(7x-1)+2y=10。通过损益术，该方程可化为：7x+2y=11。《九章算术》方程章还引入了负数，提倡正负数的加减律例，与今天的设施无异，负数的引入是数系的又一伏击扩张，是中国古代的伏击建树。

《九章算术》方程章中的“损益术”

在咋舌于中国古代数学家们取得建树的同期，咱们也应意志到古代数学常识跨好意思丽传播、演化通常并不是从一个“里程碑”到另一个“里程碑”的“辉格史”历程，而是一个极端复杂且充满多元化的历程。到当今为止，莫得凭据标明上述中国古代代数学想想影响了花拉子密。与之近似，花拉子密《代数学》中相通莫得欧几里得《几何原本》、丢番图（Diophantus，约246-330）《算术》等古希腊数学文章中的任何代数学陈迹。天然，花拉子密《代数学》在个别问题中体现了印度数学的特色，但在谈话表述、章节安排、想想呈现等方面更猛进程体现出其原创性。

古代数学常识在跨好意思丽传播、演化历程中这种非线性特色的例子还有好多。举例，15世纪初波斯数学家阿尔·卡西（al-Kāsh，约1380-1429）专揽三次方程数值解求出sin1°放纵精度值从而进步正弦表精度，但这种算法并未传入欧洲。16世纪中叶，奥地利数学家雷蒂库斯（Rheticus，1514-1574）开动致力于于求解高精度正弦表，直至半个世纪后德国数学家毕的斯克斯（Pitiscus，1561-1613）才在1595年出书的《三角法》一书中达到了近200年前卡西的建树。1631年，德国布道士邓玉函（Jean Terrenz，1576-1630）以《三角法》为原来编写《大测》传入中国时，并未将上述算法写入《大测》；直至1722年《数理精蕴》中，中国数学家才经过落寞探究并掌抓上述算法，但此时距卡西惩办此问题已已往300年。

03

花拉子密的生平与《代数学》的主要内容

花拉子密的生平信息很少，这种情况在古代知名数学家中并不是个例，比如古希腊数学家欧几里得、中国古代数学家刘徽（公元3世纪）、贾宪（11世纪）等东说念主的生平信息也很少。花拉子密全名——穆罕默德·本·穆萨·花拉子密（Muhammad ibn Mūsā al-Khowārizmī），根据阿拉伯东说念主名字的特色，他的名字应叫穆罕默德。其中“本”是男儿的真谛，是以“本·穆萨”标明他的父亲叫穆萨。临了一个单词标明他来自中亚花剌子模地区，然而他的父辈们或是更早的祖宗何时来到巴格达，咱们一无所知，只知说念他生涯在巴格达且莫得去过其他场所。花拉子密共有12部文章，这些作品题材世俗，包括数学、天文体、年代学、地形学和历史。他的数学文章除了《代数学》除外，还有一真名为《印度算术书》的文章，该书在阿拉伯世界初次系统地先容了印度十进位制记数法以及关系计较设施。

之是以省略在9世纪初的阿拉伯地区产生像花拉子密这么伟大的科学家统统不是偶而的，这是政事、经济、文化等多方面身分共同作用的逼迫。据推断花拉子密诞生在公元8世纪的临了一个十年，并在其时学风盛行的巴格达秉承讲授。阿拔斯王朝第七任哈里发马蒙（al-Ma’mūn，813-833）在巴格达修建了“灵敏宫”并开启了“百年翻译畅通”。花拉子密在这一时间被邀请到“灵敏宫”责任，完成了《代数学》并在该书弁言中抒发了对马蒙的尊敬与谢忱。直至第九任哈拉法瓦希克（al-Wāthiq，842-847在位）物化的公元847年，花拉子密仍辞世。

1983年发行的花拉子密操心邮票

花拉子密《代数学》正文分四部分：一元二次方程表面、商贸问题（三率法）、几何度量问题、遗产问题。该书开动部分便先容了由根（即一次项）、平素（即二次项）及数（即常数项）组合成的六种类型的圭臬方程：

1、平素等于根（ax^2=bx）；

2、平素等于数（ax^2=c）；

3、根等于数（bx=c）；

4、平素与根之和等于数（ax^2+bx=c）；

5、平素与数之和等于根（ax^2+c=bx）；

6、根与数之和等于平素（ax^2=bx+c，以上a, b, c＞0）。

花拉子密在构造方程时，仅探讨有正根的方程，化简得到的圭臬时势方程势必为一些正项之和等于另外一些正项之和。在保证方程存在正根的前提下，上头六种方程与今一元二次方程的圭臬时势ax^2+bx+c=0(a, b, c∈R)是等价的。前三种类型方程解法较通俗，对于后三种类型方程，花拉子密最初将二次项所有这个词化为1，然后用翰墨谈话详备讲演其求根公式，举例第五种方程极端于：

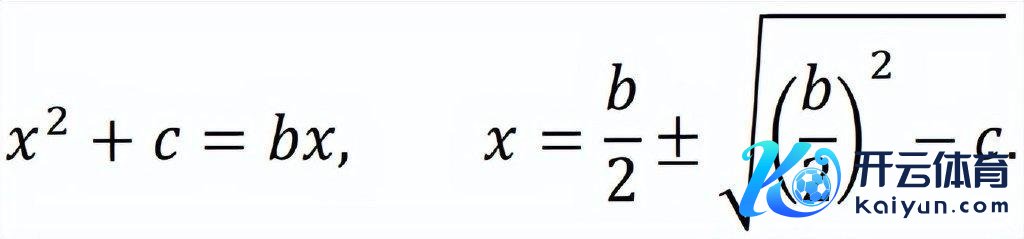
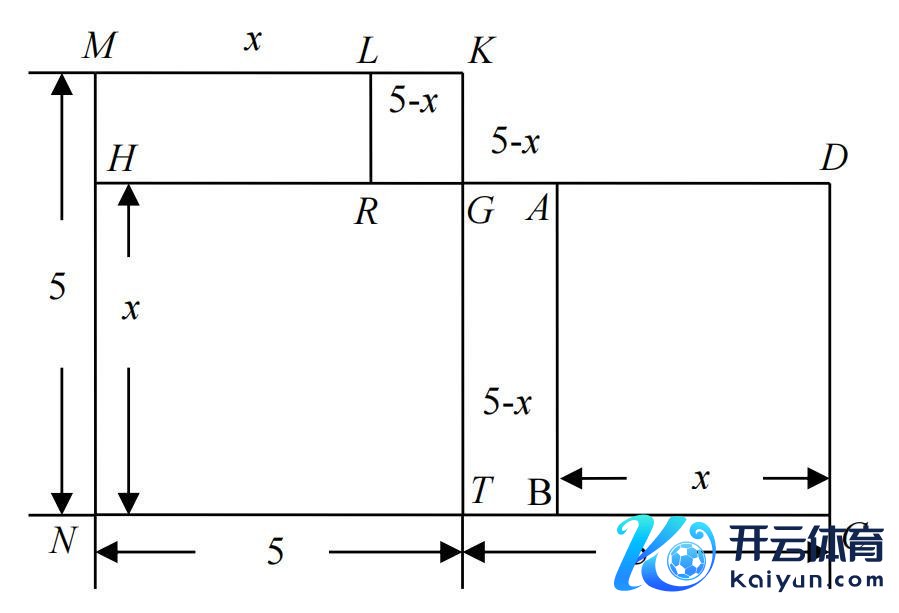
花拉子密《代数学》（1342年版）

前边所列是6个圭臬时势方程，然而根据题意列出的方程通常形态各别，是以花拉子密接下来给出了方程化简的设施，即通俗的整式运算律例。全书第二、三部分——商贸问题和几何度量问题的篇幅极端粗略，临了用了全书一半的篇幅来讲演58说念与伊斯兰遗产法关联遗产秉承问题，它们实质上是复杂的一元一次方程。底下以第一题为例，这亦然最通俗的一说念：

一个东说念主物化后留住两个男儿，并将其总遗产的三分之一遗赠送一个目生东说念主。他留住十迪拉姆的遗产，且有一个男儿欠了父亲的债务，他将不会享有这十迪拉姆（中的任何部分）。

一个男儿欠了父亲的债务，设这个男儿的债务为x，将其加父亲留住的财产后进行分拨，则总遗产为10+x。这个男儿所得的遗产与其原有的债务相抵消，则有：

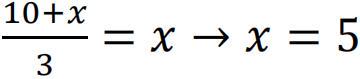
目生东说念主得到5迪拉姆，其中一个男儿得到5迪拉姆，另一个有债务的男儿所得遗产与原有债务抵消。对伊斯兰遗产法中章程的复杂遗产分拨问题进行代数求解的活动，体现了其时数学与宗教风雅的伴生关系，事实上这种伴生关系衔接了整个中叶纪伊斯兰数学发展的黄金期。与之近似的，信徒寻找面向麦加城精准办法进行祈祷而产生的“奇伯拉”问题，促进了阿拉伯三角学的快速发展。宗教中的伏击问题为数学提供了发展的能源，同期赋予了数学更高的权威与地位，这些齐体现了数学在发展历程中多元化的文化特色。

04

花拉子密《代数学》的深化影响

对于第一次阅读花拉子密《代数学》的读者而言，它似乎并莫得给东说念主目下一亮的嗅觉。这并不是一册洋洋洒洒，而是略显单薄的小册子；书中也莫得复杂的贫穷，今天的初中生阅读起来也毫无梗阻；书中莫得代数标志，全部用翰墨谈话表述，给东说念主一种“原始”的嗅觉。然而由于其中明确的方程想想阐释、实用价值和官方配景，该书很快便取得了远大的关怀。与花拉子密同期期以及稍晚的许多数学家均参与到《代数学》的深入究诘中，举例同期期的伊本·吐克（ibn Turk，9世纪东说念主）补充了花拉子密讲授一元二次方程求根公式正确性的几何讲授；稍晚些的塔比·伊本·库拉（Thabit ibn Qurra，826-901）初次将欧几里得《几何原本》与花拉子密《代数学》进行深入比较有计划；阿布·卡米尔（Abū Kāmil，约850-约930）全面秉承况兼发展了花拉子密的代数学想想。一方面伊本·吐克、塔比·伊本·库拉、卡米尔等东说念主的责任进一步明确了花拉子密的代数学想想，并为后世阿拉伯数学家在方程的化简和求解限度提供了更广宽的有计划视角和更丰富的有计划内容；另一方面，恰是由于参与了花拉子密《代数学》的有计划而使得上述数学家的名字齐刻在了数学史的“业绩簿”上。

花拉子密所著《代数学》书中的“复原与抵消”设施当作代数学的基本特征被永久保留住来，同期该书基本敬佩了后世阿拉伯代数学中方程化简与方程求解这两条主要的发展线索。最初在方程化简限度取得蹂躏性发扬的是卡拉吉（al-Karaji，953-约1029），他的责任使得代数学进一步“落寞”， 极端于系统地将加、减、乘、除、比例和开方这几种基本算术设施应用于代数抒发式。随后的萨马瓦尔（al-Samaw’al，约1130-约1180）进一步发展了凯拉吉的表面。最终，这种源于方程化简历程中的基本运算法子及通俗的算术设施在阿拉伯数学家们的费力下发展成一套相对完备的表面。

花拉子密、塔比·伊本·库拉、卡米尔等数学家们在一元二次方程的代数解、几何解、数值解等方面照旧得到相对完备的后果。而最初在一般高次方程求解限度取得蹂躏性发扬的是奥马尔·海亚姆（Omar Khayyam，1048-1131）。海亚姆最大的孝顺在于他对一元三次方程给出了基于希腊数学常识的几何解法，实质上是专揽圆锥弧线交点对方程的解进行定性边幅。最初在一般三次方程数值求解限度取得蹂躏性发扬的是萨拉夫·丁·图西（Sharaf al-Dīn al-Tūsī，约1135-1213），这为后世数学家进行高精度数值求解奠定了基础。

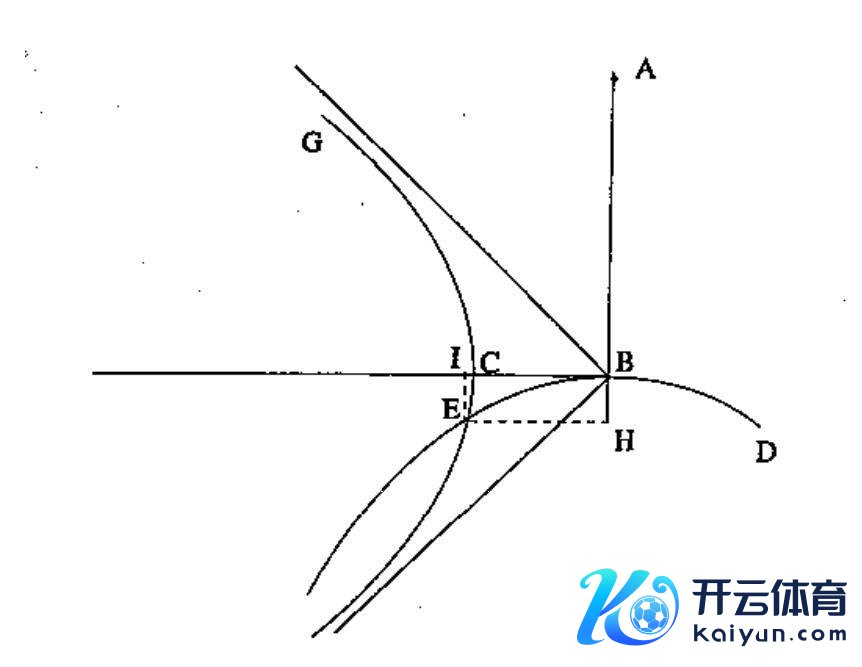
海亚姆求解x3+c=bx图示（抛物线与双弧线的交点示意方程的根）

花拉子密的《代数学》于12世纪被翻译为拉丁文并在欧洲开动传播。花拉子密的拉丁文译名其后缓缓演变为algorism和algorithm这两个英文单词，前一个单词是“阿拉伯记数法”；后一个单词成为数学中的私有名词“算法”，即惩办某种问题的特定的计较法子。

13世纪初，意大利数学家斐波那契（Fibonacci，约1175-约1250年）在代表作《计较之书》讲述了卡米尔书中的代数学内容，其中第406页边注中提到Maumeht（即穆罕默德），以明确示意二次方程的解法出自花拉子密。从13世纪开动，欧洲科学激越的原点就在于消化摄取并越过斐波那契等学者的文章。随后，许多欧洲数学家也被阿拉伯代数学蛊惑，并一直致力于于寻找一般三次方程的代数解公式。1545年，意大利数学家卡尔达诺（Cardano Girolamo，1501-1576）在德国纽伦堡出书了一部对于代数学的拉丁文文章《大术》，一般三次方程和四次方程的求根公式终于公之世人，这也标志着欧洲东说念主真的接过阿拉伯东说念主传过来的数学接力棒。欧洲数学家们经过不懈的费力，于19世纪初最终讲授了一般五次方程莫得代数解，开启了晚世代数的有计划。19世纪初，中叶纪的阿拉伯数学引起了欧洲数学史家们的关怀，花拉子密《代数学》先后被翻译为英语、法语、俄语等。

2020年笔者出书的花拉子密《代数学》中译本

参考文件

[1] Al-Khwārizmī, Edited with translation and commentary by Roshdi Rashed,The Beginnings of Algebra[M], SAQI, Landon, 2009.

[2]Martin Levey,the algebra of abu Kamil, kitab fi al-jabr wa’l-muqabala[M], in a commentary by Mordecai Finzi, Hebrew text, translation, and commentary with special reference to the Arabic text, the university of Wisconsin press: Madison, Milwaukee, and London, 1966.

[3] S.Ahmd and R.Rashed eds., al-Samaw’al,al-Bahir en algebra[M], Damascus, 1972.

[4] R.Rashed et. B.Vahabzaded.Al-Khayyam Mathematicien[M]. Paris: Librairie Scientifique et Technique Albert Blanchard, 1999.

[5]R.Rahed,Sharaf al-Din al-Tushi, CEuvres Mathematiques[M], Algebra et Geometrie au XII siècle. Collection Science et Philosophie Arabes. Paris: Societe d’edition

, 1986.(Tome I, II.)

[6] Jamshid al-Kāshī.Miftah al-Hisab (Key to Arithmetic)[M]. A S al-Demerdash.M H al-Cheikh (eds). Cairo: Dār al-kātib al-ʿarabī,1967.

[7] Bartholomæi Pitisci Grunbergensis Silesij Trigonometriæ Siue De dimensione Triangulor[um] Libri Qvinqve ; Item Problematvm Variorv[M], nempe Geodæticorum, Altimetricorum, Geographicorum, Gnomonicorum et Astronomicorum Libri Decem. Augsburg, 1612.

[8] 陈志辉.宋元数学有计划的复兴、疏导与互鉴[J].中国社会科学报.2024.1.24.A05.

特 别 提 示

1. 参加『返朴』微信公众号底部菜单“佳构专栏“，可查阅不同主题系列科普文章。

2. 『返朴』提供按月检索文章功能。关怀公众号，回应四位数构成的年份+月份，如“1903”，可获取2019年3月的文章索引，依此类推。

版权阐扬：宽宥个东说念主转发，任何时势的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内推断后台。